The group that starts with the Equations keyword is used to define linear combinations of the measured motions. The slave node equations can be used for definitions of rigid body motions and slave nodes. This is very helpful when the mode shapes are animated. Even though the measurements are only available in few nodes of the geometry the equations can be used to make the complete geometry move.
Each record in the group contains only one field which is a string of any length. This string is one equation, which imply that equations must be defined in one line only. All equations start in the same way as shown below:
node( <Node Number>, <Direction> ) =
This equation defines the motion of the node specified by <Node Number> in the direction specified by <Direction>. The <Direction> field is a number from 1 to 3. 1 corresponds to X direction, 2 corresponds to Y direction and 3 corresponds to Z direction.
Note: To define that the motion is in the negative direction it must be performed on the right-hand side of the equation sign. In other words, the motion in one direction of a node must always be done in the positive direction.
If you want to set the nodes motion in a specific direction to static values you can simply write an equation like
node( <Node Number>, <Direction> ) = 3.1415926535
This equation sets the motion of the node specified by <Node Number> in the direction specified by <Direction> to pi. Incidentally, pi is actually the only predefined constant available which means that in the present case you also write:
node( <Node Number>, <Direction> ) = pi
You can also make a nodes motion in a specific direction a linear combination of other nodes by writing an equation like
node( <Node Number 1>, <Direction 1> ) = |
1.5*node( <Node Number 2>, <Direction 3> ) + 2*pi - cos( node( <Node Number 4>, <Direction 2> ) ) |
This equation sets the motion of the node specified by <Node Number 1> in the direction specified by <Direction 1> equal to a motion that is a linear combination of the motion of <Node Number 2> in <Direction 3> and the cosine of <Node Number 4> in <Direction 2>. Please note that the splitting of the equation into two lines as shown above is not allowed in ARTeMIS Extractor.
The following functions are available and can be used with numerical or functional arguments:
node( <Node Number>, <Direction> ) |
Returns the motion node <Node Number> in direction <Direction>. |
sqrt( x ) |
Returns the square root of the input argument x. |
sin( x ) |
Returns the sine of the input argument x. |
sinh( x ) |
Returns the hyperbolic sine of the input argument x. |
cos( x ) |
Returns the cosine of the input argument x. |
cosh( x ) |
Returns the hyperbolic cosine root of the input argument x. |
log( x ) |
Returns the natural logarithm of the input argument x. |
The following operators and predefined constant are available:
* |
Muliplication |
+ |
Addition |
- |
Subtraction |
/ |
Division |
pi |
The number Pi = 3.141592653589793108624468950438 |
() |
Brackets with possibility to have up to 20 bracked terms inside each other. |
For the building model example the group of equations is like this:
Equations
node(8,1) = node(11,1)
node(8,2) = node(2,2)
node(11,2) = node(5,2)
node(9,1) = node(12,1)
node(9,2) = node(3,2)
node(12,2) = node(6,2)
node(5,1) = node(11,1) - node(2,2) + node(5,2)
node(2,1) = node(5,1)
node(6,1) = node(12,1) - node(3,2) + node(6,2)
node(3,1) = node(6,1)
Here the motion of node 8 in direction 1 (x-direction) is defined to be equal to node 11 direction 1. A more sofisticated example is that the motion of node 5 in direction 1 is specified as:
node(5,1) = node(11,1) - node(2,2) + node(5,2)
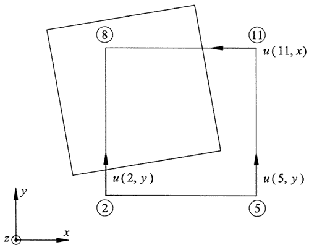
In order to understand the equations in the example, consider the following figure illustrating the movements of one of the deck plate in the building model:

It is assumed that the deck plate moves as a rigid body, i.e. the movement can be described by two displacements and one angle. The deformation angle is given by:
![]()
where a is the depth of the plate. Now, assuming the plate is moving like a rigid body, the deformation in the x-direction of the lower right corner of the plate is given by
![]()
or if we introduce the formula for the angle
![]()
and this is what the 7th equation says. Exchange u(5,x) with node(5,1), u(5,y) with node(5,2) etc. and you arrive at the equation in the 7th line. The idea is simply to specify the motions of the nodes that are not defined directly from the measurements by the rigid body motions.
If you want to postpone the equation definition or if you have found an error you can always reload the equations from the File menu. You will then be asked to specify a SVS Configuration File containing the equations to be loaded. In this case you can still use you existing configuration file now with equations added or modified. However, in the file you load only the Equations group needs to be present.
You can also add the equations directly in the Slave Node Equations Editor in the Mode Organizer Editor at any time after the project has been created and compile them immediately.